数据工程师告诉你：遇见Mr. Right需要相亲多少次？ -开智学堂的财新博客-财新网

苏格拉底问题

谈到相亲就不得不提到著名的麦穗问题。话说有一天，苏格拉底带领几个弟子来到一块成熟的麦地边。他对弟子们说：

你们去麦地里摘一个最大的麦穗，但要求只能摘一次，只许进不许退，我在麦地的尽头等你们。

可以看得出，相亲这种活动就有点类似于摘麦穗，在等待和决断之间达成平衡是解决问题的重点。

将上述的麦穗问题进一步抽象就是一个经典的概率问题。

对于这个概率问题，一种思路就是取 1 到 100 之间的某个数字 n，以它作为分割点将整袋球划分为两组，

我们以第一组为观察对象，找到第一组中最大的球 M，记录其大小但并不行动。然后从第二组中寻找大于 M 的第一个球，取该球为最终选择。

那么 n 应该设为多少，才能使取到最大球的概率尽可能的高呢？

Ross 在其《概率论基础教程》中已经给出了精确的解析（英文版第 8 版 P345；或者陈木法的《随机过程导论》 P105），最优的 n 公式表达为：

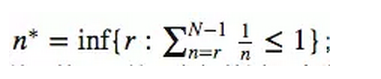
在 N 充分大时，n 应该取在 1/e 的比例处，也就是所有球数目的 37% 处。

在解的过程中先运用条件概率得到全概率表达式，再用连续化的积分来近似离散化的概率，将积分求出后进行求导得到最终答案。看到这里各位是否有些惊讶，这个 e 可是无所不在啊。

换句话说，如果你确定在生命中会遇到 100 个对象，那么对前 37 个就请按捺住你的热情，判定其中最优秀的那位 M，然后再去寻找比 M 更优秀的，如果真的遇到就立刻行动，不要再犹豫。因为她/他很可能就是 Mr. Right。

口说无凭，我们用 R 语言来检测一下上面的结论。

从下图可以看到最大值的确取在 37 附近，符合理论结果。

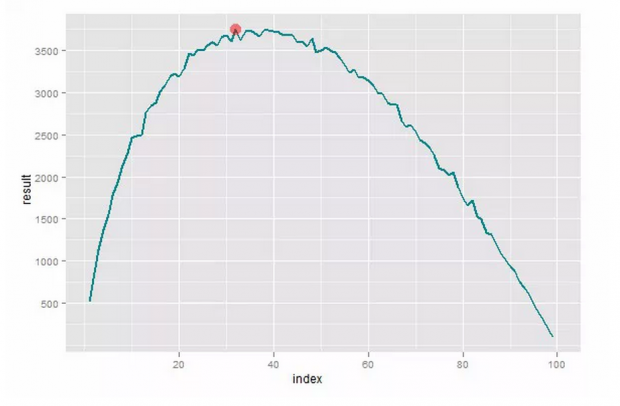
横轴表示了不同的划分参数 n，纵轴表示给定 n 条件下，能得到最优值的频数

这里还有一个问题，最优解不一定是令人满意的。根据最优解来行动，会有 36% 的可能得到最佳的对象，但也有接近 38% 的可能会一无所获。

实际上，有时候我们宁可得到一个次优的结果（例如 99）也不希望孤独的生活。

所以在选择 n 这个参数的时候，目标应该着重于结果的期望值大小。重新编程运行后，从下图可以观察到最优值取在 7 附近。

也就是说，如果你确定在生命中会遇到 100 个对象，那么前 7 个就略过，判定其中最优秀的那位 M，然后再去寻找比 M 更优秀的，这样有最大的可能得到靠谱的对象。

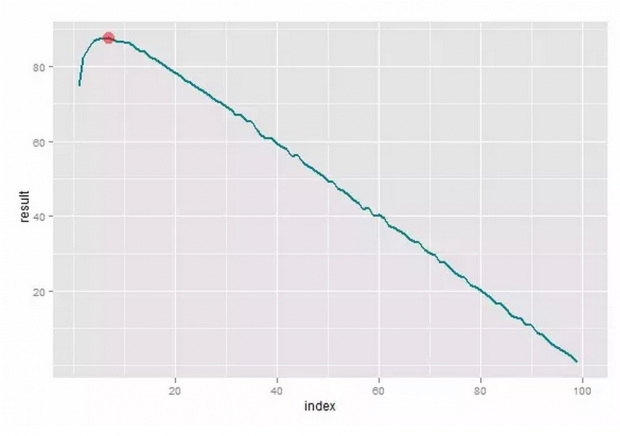
横轴为不同的划分参数 n，纵轴表示 10000 次模拟的期望值

好了，我们知道了应该在观察 7 个对象后就开始行动，那么需要多少次相亲才能碰上 Mr. Right 呢？

我们先构造一个函数来记录在第二组中进行尝试的次数。然后模拟 10000 次后绘制直方图如下，

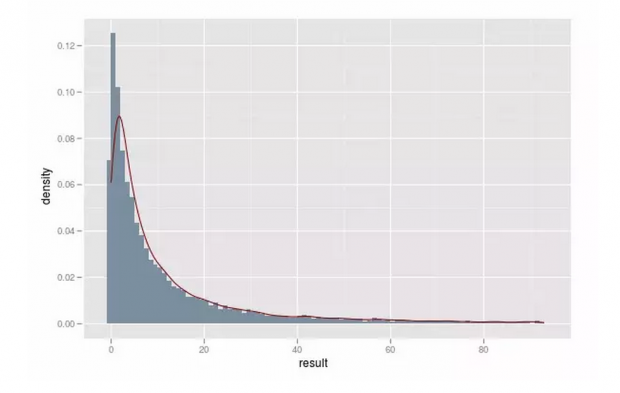
可以看到：

所以说，只要你人品不是太差，在 37 次相亲尝试之内，应该就可以找到靠谱的对象。但愿你不会掉入离群点中去。

进行对象选取的一万次模拟，每次模拟返回选取对象所需要的尝试次数，0 表示未能得到任何对象，1 表示在观察七个对象后，只需要一次尝试就得到较优的对象。

完整的 R 代码如下：http://t.cn/RAVckVm ；相关维基百科讨论请参考「Secretary problem」条目。■

注：本文结论有很多隐藏前提，其推理亦可能有失误之处，仅供娱乐。若读者完全以本文为指导进行相亲活动，后果概不负责。

话题：